藍影

割線法是在曲線上先任取二點，
求出這二點之割線直線方程式與x軸之交點，
而割線直線方程式應用到了
拉格南奇插值公式
拉格南奇插值公式
設 xy 平面上有 n+1 個點, 分別為
(x0,y0), (x1,y1)....(xn,yn)
則通過此 n+1 個點之方程式為

 明
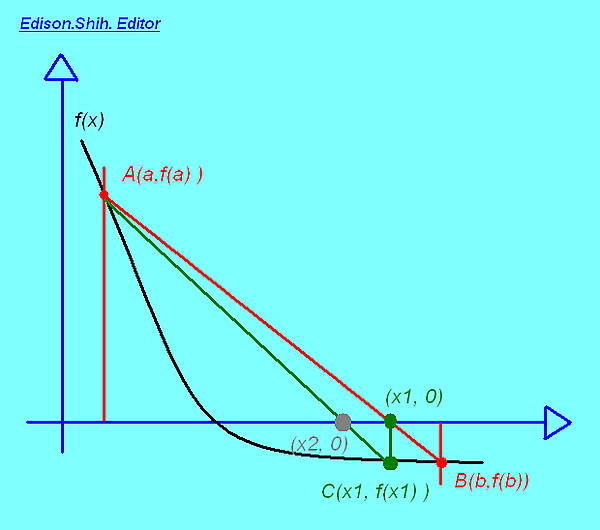
設 f(x) = 0 於 [a,b] 有一解存在，步驟如下
(1) 將 a b 二點對應之 f(x) 求出,
    對應之點為 A (a, f(a)), B (b, f(b)) 二點
(2) 求通過 A, B 二點之直線方程式,
    運用 y=mx+k 之公式, 求其 m 與 k, 可求得
    m = (f(a) - f(b)) / (a-b), k = (af(a)-bf(a))/(a-b)
(3) 令此直線方程與 x 軸之交點為 x1, 即 mx1+k=0,
    可化簡求得 x1 = a + f(a)(b-a) / (f(a)-f(b))
(4) 將 x1 代入 f(x), 若 f(x1)=0, 則 x1 為解,
(5) f(x1)!=0,
      (5.1) f(a)*f(x1)<0成立, 新區間為 [a,x1]
      (5.2) f(a)*f(x1)<0不成立, 新區間為 [x1,b]
(6) 直到 f(x) < EPS 結束

在了解 如何判定解區間 後
接下來要找的是
在這個解區間裡要如何找出正確解
可以用最笨的暴力法
do{
   x := x + step;   
}while(f(x) > error_rate);

以下程式碼運用了以下概念
若 f(x) 在 (a,b) "恰有一解"
則 f(a)*f(b) < 0
注意，在 (a,b) 中一定要是 "恰有一解"
如果有二個解以上的話, f(a)*f(b)<0 未必成立
故我若要知道 f(x) 於區間 (-5, 5) 內有幾個解
必需要先設一個 step, 這個 step 要保證夠小,
能夠滿足每次切開的區間都只有一個解.