 明
明
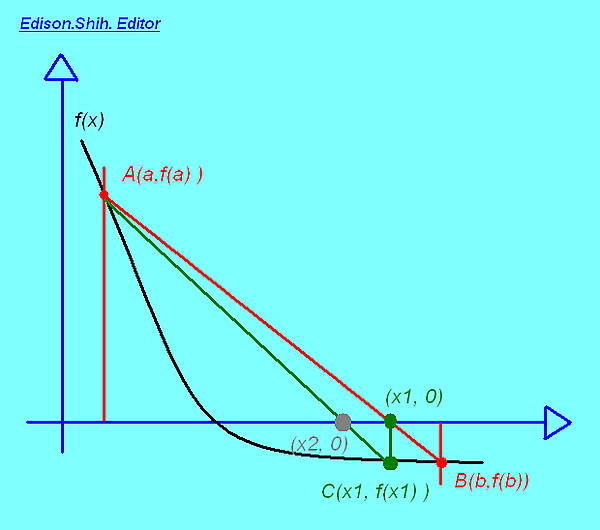
設 f(x) = 0 於 [a,b] 有一解存在,步驟如下
(1) 將 a b 二點對應之 f(x) 求出,
對應之點為 A (a, f(a)), B (b, f(b)) 二點
(2) 求通過 A, B 二點之直線方程式,
運用 y=mx+k 之公式, 求其 m 與 k, 可求得
m = (f(a) - f(b)) / (a-b), k = (af(a)-bf(a))/(a-b)
(3) 令此直線方程與 x 軸之交點為 x1, 即 mx1+k=0,
可化簡求得 x1 = a + f(a)(b-a) / (f(a)-f(b))
(4) 將 x1 代入 f(x), 若 f(x1)=0, 則 x1 為解,
(5) f(x1)!=0,
(5.1) f(a)*f(x1)<0成立, 新區間為 [a,x1]
(5.2) f(a)*f(x1)<0不成立, 新區間為 [x1,b]
(6) 直到 f(x) < EPS 結束
假位法雖然比二分法運算次數還來得少
但精準度卻沒比二分法來得好
以下為原始碼, 若有問題, 歡迎回覆討論
// ==================================
// filename: FalsePosition.cpp
// use false position method to find solution
// author : Edison.Shih.
// Date : 2010.3.7
// ** all rights resever **
// ==================================
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define EPS (double)(10E-4)
#define NO_FIND_NUM (double)(-9999.0)
// =======================================
// f(x) = x^3 + 2x^2 -5x +1,
// have sol at (-4, -3), (0,1), (1, 2)
double func(double x){
return (x*x*x + 2*x*x - 5*x + 1);
}
// =======================================
double FalsePosition(double (*fptr)(double),
double low,
double high,
double small)
{// small: error rate
double lvalue;
double hvalue;
double x=0.0, y=0.0;
//printf("========================\n");
do{
lvalue = (*fptr)(low);
hvalue = (*fptr)(high);
x = low + lvalue*(high-low)/(lvalue-hvalue);
y = (*fptr)(x);
//printf("x = %lf, y=%lf\n", x, y);
if(y==0.0) return x; // find solution
if(y>0.0 && lvalue>0.0 && hvalue<0.0) low = x;
else if(y<0.0 && lvalue<0.0 && hvalue>0.0) low = x;
else if(y>0.0 && lvalue<0.0 && hvalue>0.0) high = x;
else if(y<0.0 && lvalue>0.0 && hvalue<0.0) high = x;
else return NO_FIND_NUM;
}while(fabs(lvalue)>small && fabs(hvalue)>small);
printf("x=%lf, y=%lf\n", x,y);
return x;
}
// =======================================
int main(int argc, char **argv)
{
double sol = 0.0;
for(double x=-5.0; x<=5.0; x=x+1.0)
{
sol = FalsePosition(func, x, x+1.0, EPS);
printf("sol at (%.0lf,%.0lf):",x,x+1);
if(sol==NO_FIND_NUM) {
printf("no find sol\n");
}
else {
printf("%.4lf\n",sol);
}
}
return 0;
}
// =======================================
執行結果
sol at (-5,-4):no find sol
sol at (-4,-3):-3.5070
sol at (-3,-2):no find sol
sol at (-2,-1):no find sol
sol at (-1,0):no find sol
sol at (0,1):0.2219
sol at (1,2):1.2851
sol at (2,3):no find sol
sol at (3,4):no find sol
sol at (4,5):no find sol
sol at (5,6):no find sol



 留言列表
留言列表


